Moduł sprężystości wzdłużnej (E) jest jedną z kilku cech sprężystości materiału, charakteryzuje on opór, jaki materiał stawia wydłużeniu sprężystemu. Innymi cechami sprężystości materiału jest współczynnik Poisson’a (ν) oraz moduł sprężystości postaciowej (G) – moduł Kirchoff’a. Moduł Younga jest bardzo istotną daną dla konstruktorów, ponieważ razem z grubością elementów wpływa na sztywność konstrukcji.
Moduł sprężystości wzdłużnej (elastic modulus) zwany również jako moduł Younga jest ilorazem naprężenia normalnego (σ) i odkształcenia linowego (ε) w danych warunkach. W prawie Hooke`a stanowi współczynnik proporcjonalności pomiędzy odkształceniem a naprężeniem.
Moduł Younga wyraża się wzorem:
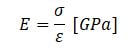
Moduł Younga dla takich materiałów metalowych jak magnez, stopy aluminium, brązy i tytan nie przekracza 150 000 MPa (150 GPa), natomiast dla stali, stopów na bazie niklu, moduł sprężystości jest większy niż 150 000 MPa (150 GPa). Średnie wartości modułu sprężystości dla wybranych materiałów podano w poniższej tabeli.
Tabela 1 Średnia wartość modułu Younga (E) dla wybranych materiałów
| materiał | moduł Younga (E) [GPa] |
| stopy berylu | 245 |
| stale | 210 |
| stopy tytanu | 110 |
| CFRP jednokierunkowe | 120 |
| stopy aluminium | 70 |
| stopy magnezu | 45 |
| GFRP jednokierunkowe | 39 |
| AFRP jednokierunkowe | 31 |
| drewno | 12 |
| lit | 12 |
Dla materiałów izotropowych występuje zależność pomiędzy współczynnikiem Poisson’a (ν), modułem sprężystości postaciowej (G) – moduł Kirchoff’a i modułem odkształcalności objętościowej (K) – moduł Helmholtza.
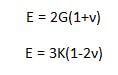
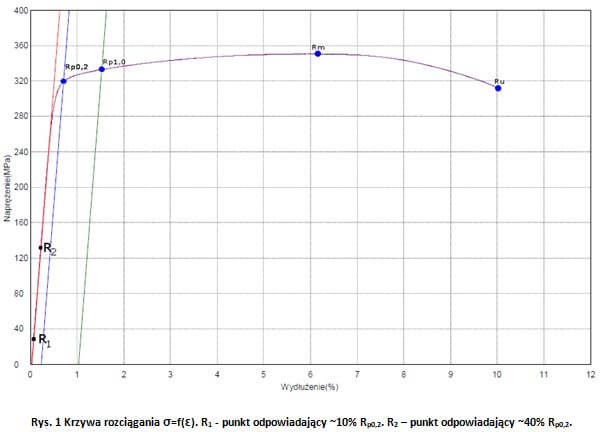
Wyznaczanie modułu Younga może odbywać się zgodnie ze sposobem opisanym w PN-EN ISO 6892-1:2020-05. W badaniu wykorzystuje się jednoosiową maszynę wytrzymałościową o klasie dokładności co najmniej 1 według ISO 7500-1 oraz ekstensometr o klasie dokładności co najmniej 0,5 według ISO 9513. W trakcie przeprowadzania statycznej próby rozciągania w zakresie stosowalności prawa Hooke`a, można określić moduł sprężystości wzdłużnej z zastosowaniem regresji liniowej, w przedziale odpowiadającym od około 10% ReH lub Rp0,2 dookoło 40% ReH lub Rp0,2.
Uproszczony przebieg wyznaczenia modułu Younga:
- Określenie przekroju początkowego próbki do badań z dokładnością do 0,5% lub lepszą.
- Wykonanie statycznej próby rozciągania w celu wyznaczenia ReH lub Rp0,2 badanego materiału.
- Przeprowadzenie kolejnych statycznych prób rozciągania z wykreśleniem wykresu naprężenie w funkcji odkształcenia w celu określania modułu Younga. W zależności od wybranej metodyki badanie przeprowadza się w zakresie nieprzekraczającym 50% ReH lub Rp0,2 na drugiej próbce lub przy przekroczeniu tego zakresu na drugiej i kolejnych próbkach.
- Na podstawie danych uzyskanych po przeprowadzeniu statycznych prób rozciągania, przeprowadza się ich analizę, z wykorzystaniem regresji liniowej. Współczynnik determinacji (R2) dla wyznaczonego równania regresji powinien wynosić co najmniej 0,9995, a współczynnik zmienności (CV) powinien być mniejszy niż 1%.
Raport z badań powinien zawierać co najmniej:
- Rodzaj zastosowanego ekstensometru.
- Wartości R1 i R2 lub ε1 i ε2.
- Liczbę zmierzonych wartości pomiędzy R1 i R2 lub ε1 i ε2.
- Moduł Younga z dokładnością do 0,1 GPa.
- Niepewność pomiaru z podaniem informacji o metodzie jej oszacowania oraz poziom ufności.
- Współczynnik determinacji (R2) lub odchylenie standardowe lub współczynnik zmienności (CV).
W przypadku próbek, dla których współczynnik determinacji (R2) dla wyznaczonego równania regresji jest mniejszy niż 0,9995 lub na wykresie nie ma prostej linii zakresu sprężystego np. dla żeliw, moduł Younga nie powinien być określany.
Normy określające wyznaczenie modułu Younga metali to m.in.:
- PN-EN ISO 6892-1 Metale – Próba rozciągania – Część 1: Metoda badania w temperaturze pokojowej
- ASTM E111 Standard Test Method for Young’s Modulus, Tangent Modulus, and Chord Modulus
- SEP 1235: Determination of the modulus of elasticity on steels by tensile testing at room temperature
Źródła:
- Oczoś K. E., Kawalec A., Kształtowanie metali lekkich, Wydawnictwo Naukowe PWN, Warszawa 2012.
- Muzykiewicz W., Wieczorek M., Mroczkowski M., Pałka P., Kuczek Ł., Moduł sprężystości wzdłużnej blachy stalowej z perforacją prostą, Obróbka Plastyczna Metali, vol. XXVII nr 4 (2016), s. 283-300.



